1 次 関数 の グラフ
この関数のグラフ {(, ⋯,,) ∈ + ∣ = (, ⋯,)} は、 (n + 1)-次元ユークリッド空間 R n+1 において超平面( 余次元 (英語版) 1 のアフィン部分空間)を描く。このような函数に対しても、上に述べたことは(平面における各概念の高次元における適当な対応物を.

1 次 関数 の グラフ. ということだ。 なぜなら、 一次関数のグラフはゼッタイに直線になるからね。 2点をむすべば直線がかけちゃうんだ。 ってことは、. 二次関数の y=ax^2+bx+c というグラフを作成してみたいと思います。 定数の a と b と cを変更することができるように、下図のようなデータリストを作成しました。. 問題1 次の1次関数のグラフについて,傾きと切片を求めてください. (各々,右の選択肢から選んでください.) 問題は8題あります. 間違ったときは Help を押す 次の問題を出すには Next を押す グラフ 1 / 8 Next.
グラフ用紙 a4に12個(pdf) a4の1ページに12個のグラフが印刷されます。小さめのグラフ用紙です。 慣れてきたらこちらが使いやすいと思います。 中学生が関数の勉強をする際に利用できるグラフ用紙を作成しました。. グラフの練習用に> 方眼紙、 グラフ用紙(算数用)、 グラフ用紙(数学用) 1次関数のグラフを描く・読み取る. 1次関数のグラフ 比例をグラフで表現したように、もちろん \(1\) 次関数もグラフに表すことができます。 \(1\) 次関数のグラフの具体例をみて見ましょう。 \(y=2x+3\) のグラフは下図のようになります。 どうして、上のようなグラフになるのか確認しておきましょう。.
2次関数と1次関数のグラフ問題で質問です。 関数y=x^2のグラフと、関数y=x+2のグラフが2点A,Bで交わっています。 交点A、Bの座標を求めて下さい。 解説には、交点ではy=x^2と、y=x+2が一致しているので、お互. 1次関数とグラフのポイントは! ・1次関数とは、 y と x が y = a x + b の式で表される関係のこと。 ・x の係数 a を「傾き」 b を「切片」という!. 1次関数との交点の座標の求め方と、グラフから読み取り直線の方程式を求める方法です。 ここでは1次関数に限定して直線と直線の交点を求める問題を取り上げて説明します。 交点を求める問題は1次関数だけでなく高校の数学でも必ず必 ….
第4節 1次関数の特徴 ☆ 前節では、1次関数y=2x+1を例にとり、1次関数を表現する方法について考えてきま した。そして、式、グラフ、表を用いることで、xの1次関数yのようすを表現するこ とができました。. 直線の式 ax+by+c=0 2元1次方程式 ax+by+c=0のグラフは直線になる。 yについて解くとy= - a b x-c b となり、傾き-a b 、切片 - c b の1次関数のグラフになる。 a=0のときは、変数がyだけでy=kの形の式になり、b=0のとき、変数がxだけで、x=hの形になる。. 例 1次関数y=2x-3でxの変域が-1≦x≦4のときのyの変域を求める。 4-1-5 5 y=2x-3のグラフ(全域) >>グラフ.
1次関数のグラフ y=axとy=ax+bを比べてみると、x=1としたときにy=axはy=a、y=ax+bはy=a+bの値をそれぞれとります。 つまり、同じxの値に対してyの値が「+b」になるのです。 これが意図することは、1次関数y=ax+bのグラ. 1次関数 y= a x+b のグラフの傾きは a ,切片は b です. (1) 切片 は, y 軸との交点(の y 座標)という「目に見えるもの」なので,切片の意味を間違う生徒は少ないです.. A, cを定数として、関数y=ax+cのグラフは直線になります。これを 直線y=ax+c といい、y=ax+cをこの 直線の方程式 といいます。.
これで一次関数y=3xのグラフが書けました!今回は点(2 , 6)をとりましたが、x=1のときはy=3なので、点(1 , 3)と原点を通る直線を引いても問題ありません。 次からは、一次関数y=ax+bのグラフの書き方を解説します。 一次関数のグラフの書き方:y=ax+bの場合. Y = 3 x – 5 のグラフを描いてみることにします。 ソースコードはとても簡単!わずか8行(実質6行)です。 liner_function.py import numpy as np # NumPy を読み込む import matplotlib.pyplot as plt # Matplotlib を読み込む x = np.arange(-10, 10, 0.1) # x座標を-10 から 10 まで 0.1 きざみで取得 y = 3 * x. この映像授業では「中2 数学 1次関数3 グラフの書き方1」が約6分で学べます。問題を解くポイントは「y=ax+bのグラフは、2点を求めて直線で.
1次関数のグラフ1 *まずは比例のグラフ y=ax から平行移動する練習をします。 y=ax+bのグラフを書く場合.y=ax のグラフを書く 1のグラフをbの分だけ上下に移動する。(+なら上、ーなら下へ) よく分からない場合は、 比例のグラフ を復習しましょう。 1次関数のグラフ2. 「1次関数のグラフ」 を 解説していきますね。 原点の代わりとなる点はどこ? 中2数学の「1次関数」とは、 「y = a x + b 」 という式で表される 関数のことですが、 1次関数のグラフは、 比例のグラフに似ている所があります。 すなわち、. ③\(\displaystyle{y=-\frac{1}{2}x}\)はパッと見たところ、一次関数ではないように見えますが…これは\(a=-\frac{1}{2}, b=0\) になっている一次関数の式です。 ④\(y-4=2x^2\) は式を変形して、\(y=2x^2+4\) の形にすると\(x\)が二乗になっていて、二次式になっていることが.
1次関数のグラフ2
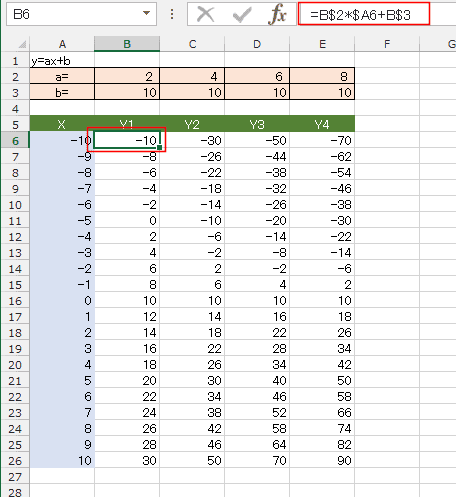
一次関数 二次関数のグラフや円のグラフを作成したい エクセル13基本講座
1次関数のグラフ4
1 次 関数 の グラフ のギャラリー

1次関数 グラフから直線の式を求める 勉強ナビゲーター
1次関数のグラフ1

中学2年生の数学 1次関数と正方形 長方形 塾講師が数学をやりmath

一次関数とは 式とグラフの解説 数学fun

中2数学 1次関数のグラフの書き方 例題編 映像授業のtry It トライイット

1次関数のグラフの書き方 切片について 勉強ナビゲーター
Q Tbn 3aand9gcth1g4atk8n1u1ljuqtfxn3ozjjt3p7sfi8vqfblwn9gvgjfbgk Usqp Cau

一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
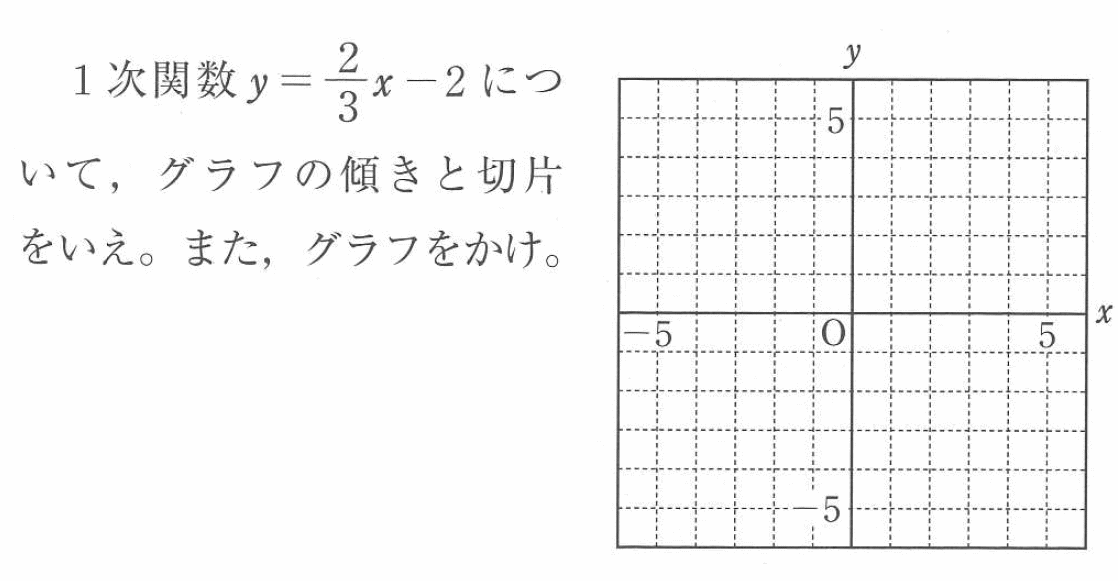
Studydoctor一次関数のグラフと傾きと切片 中2数学 Studydoctor
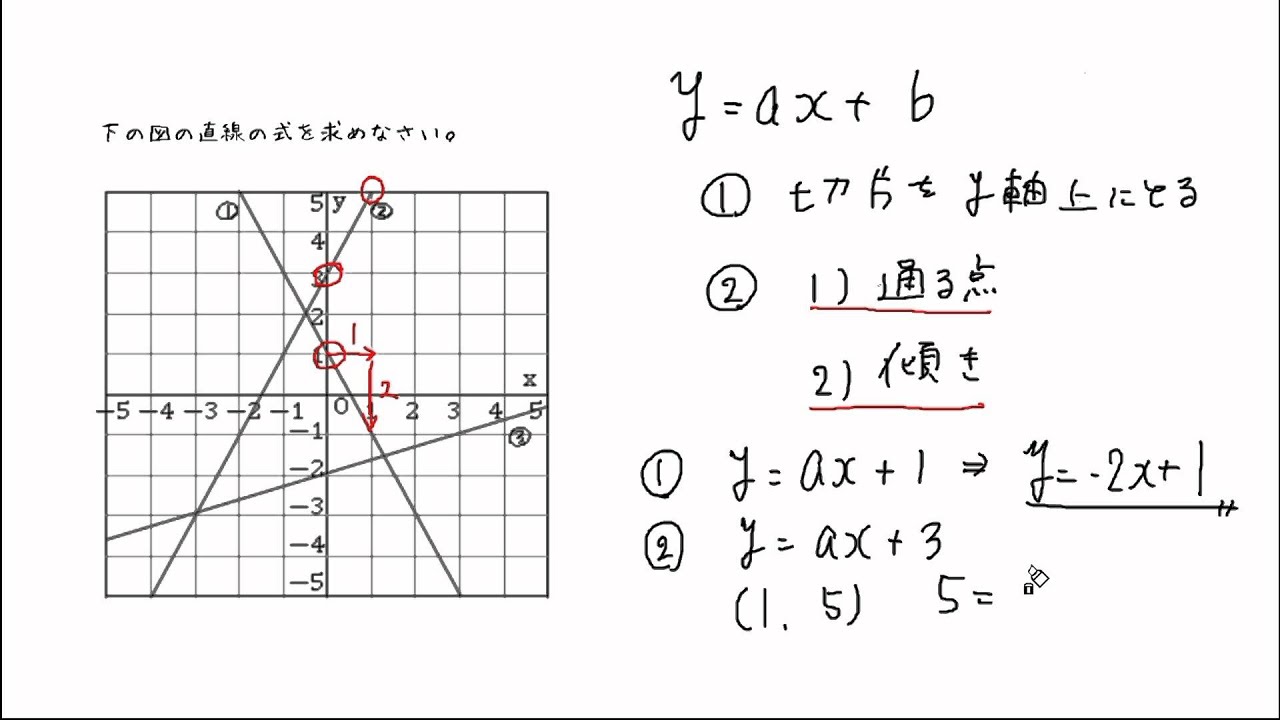
グラフから一次関数の式をもとめる Youtube

数学中二 一次関数 方程式とグラフ 中学数学に関する質問 勉強質問サイト

Y Ax Bのグラフと 切片と傾きの意味 中学数学 By じょばんに マナペディア
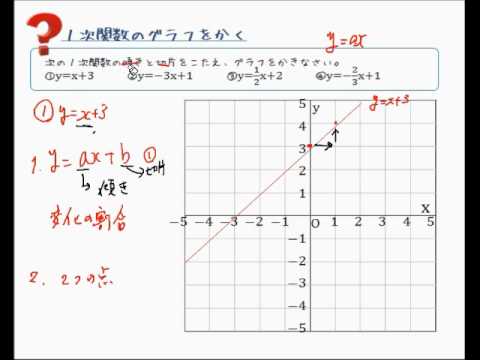
1次関数のグラフのかき方 Youtube
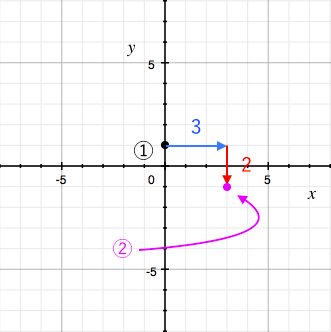
一次関数 グラフの書き方 苦手な数学を簡単に

1次方程式と1次関数の関係 数学 二次関数 数学公式まとめ大全
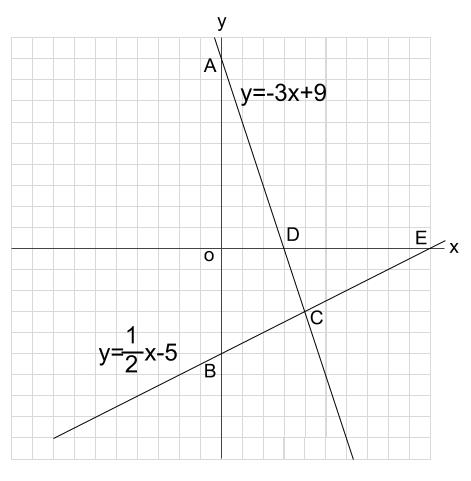
中学数学 1次関数と三角形の面積 その1 中学数学の無料オンライン学習サイトchu Su
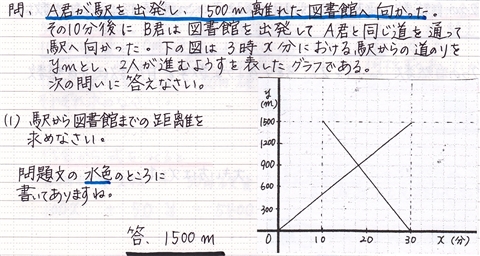
中学の一次関数 2次関数の勉強のコツを知って得意になろう

一次関数の傾きと切片を求める問題 Irohabook
数学 スタディーx

1次関数のグラフ やややさしい数学
Wordで使える 中学数学のグラフ用紙 Wordで数学問題プリントを作ろう
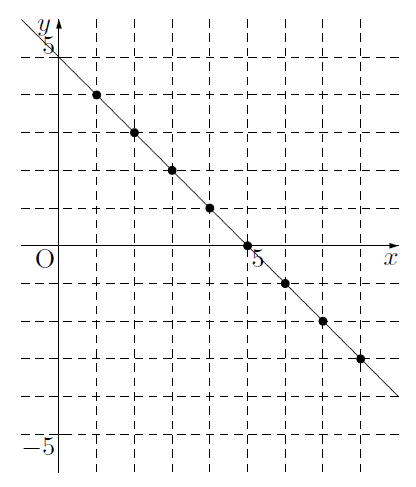
2元1次方程式のグラフ まなびの学園

一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく

1次関数3 1次関数のグラフの交点と連立方程式の解 身勝手な主張

基礎数学 3回目
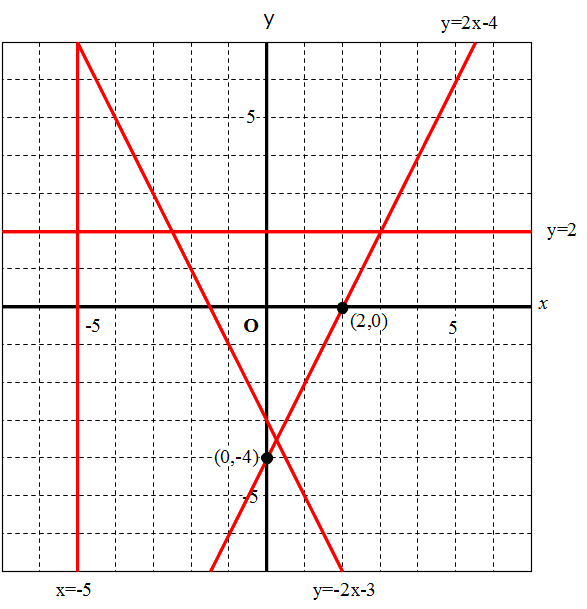
Math 超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 働きアリ
中2数学 1次関数 指導案 動点とグラフのわかりやすい授業
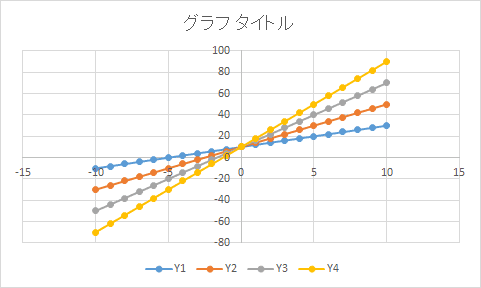
一次関数 二次関数のグラフや円のグラフを作成したい エクセル13基本講座

比例 反比例 一次関数 二次関数 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信

1変数一次関数 数学についてのwebノート

中学2年生 数学 1次関数 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
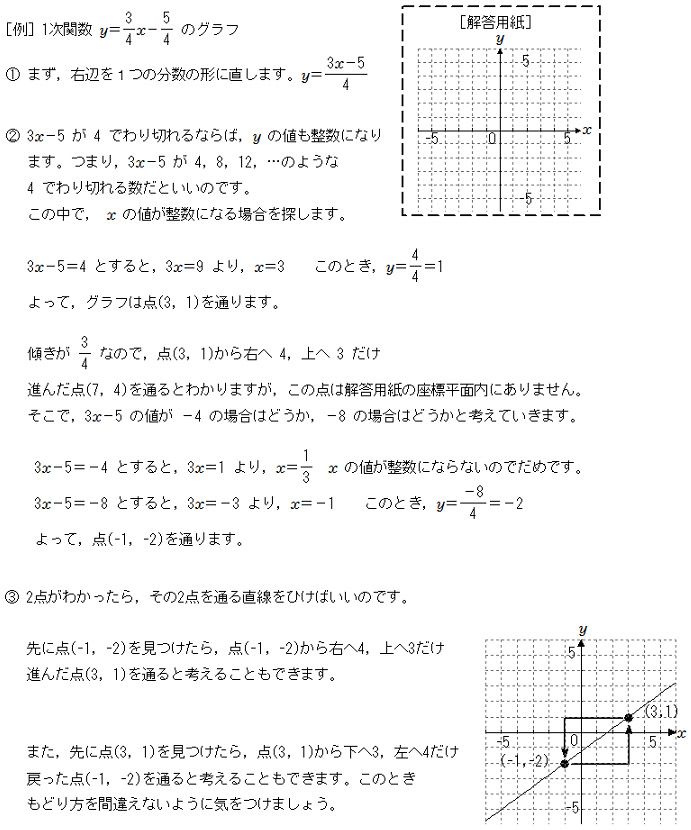
1次関数 傾きや切片が分数であるグラフのかき方 中学数学 定期テスト対策サイト
9 1 1次関数 グラフの描き方 読み取り方 勉強できようサイト
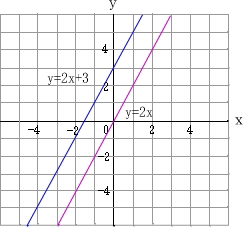
1次関数のグラフ 中学から数学だいすき

中学2年数学練習問題 一次関数の利用 速さ 時間等の文章問題
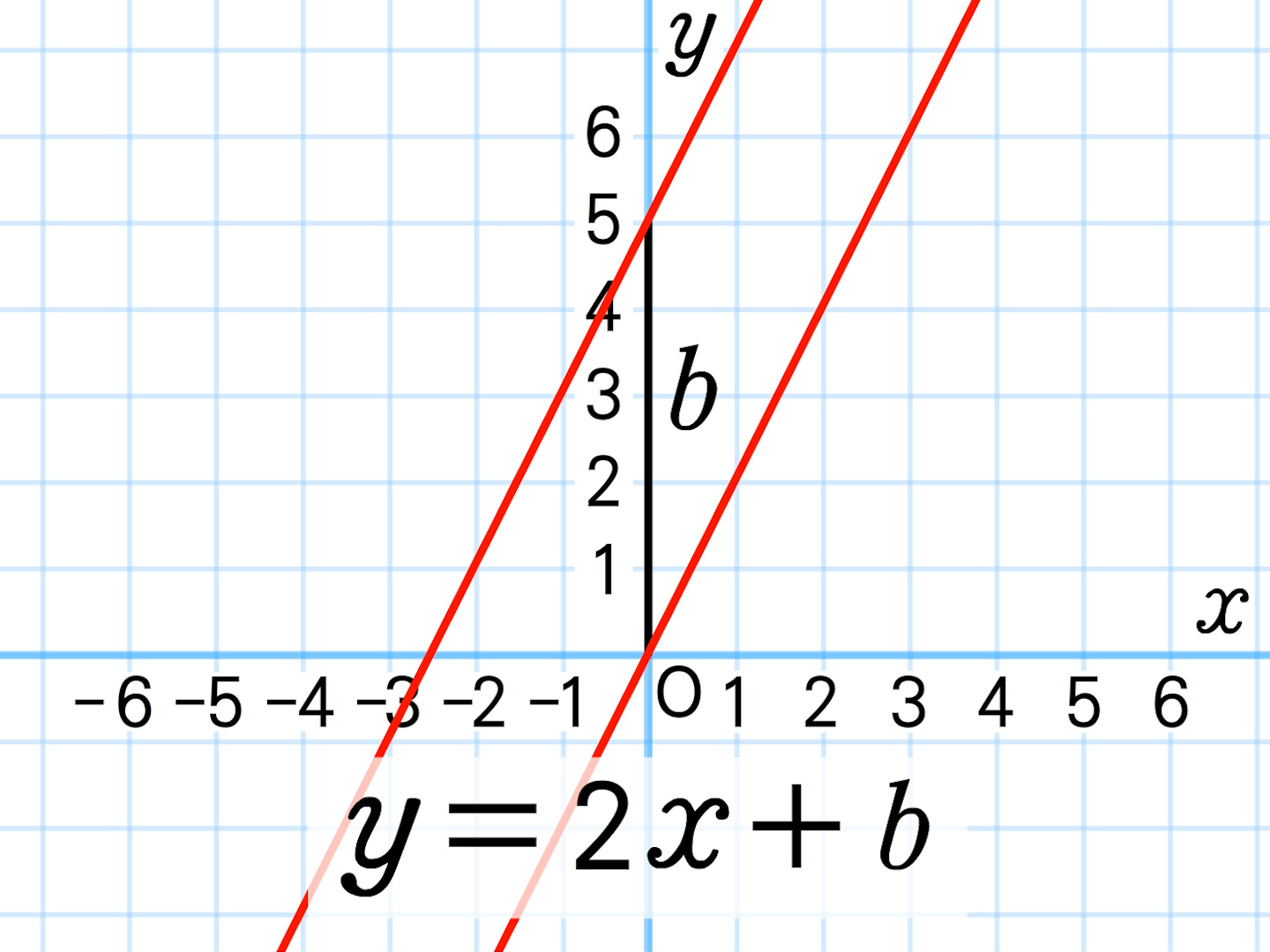
2年 1次関数のグラフ 1 数学イメージ動画集 大日本図書
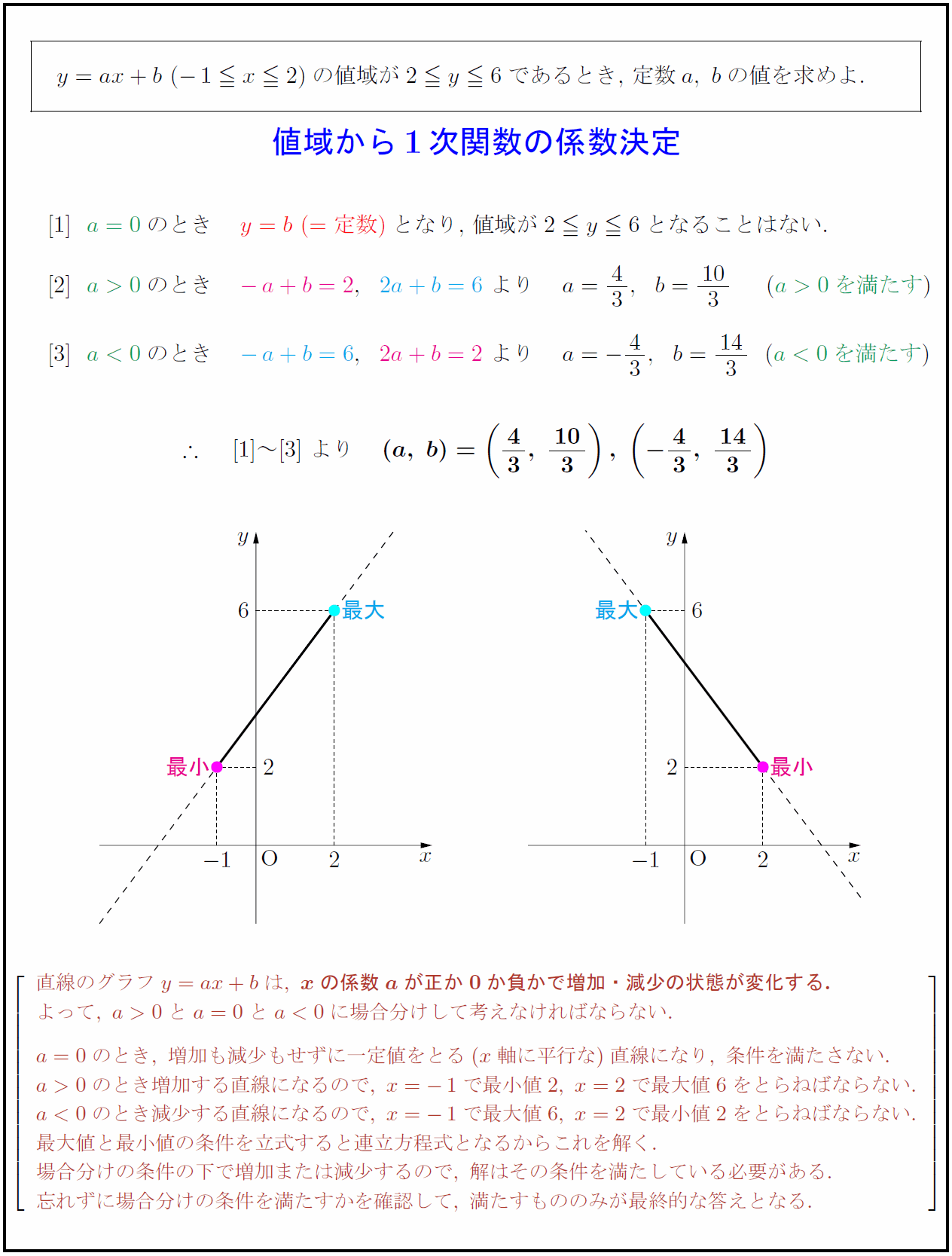
高校数学 値域から1次関数の係数決定 受験の月
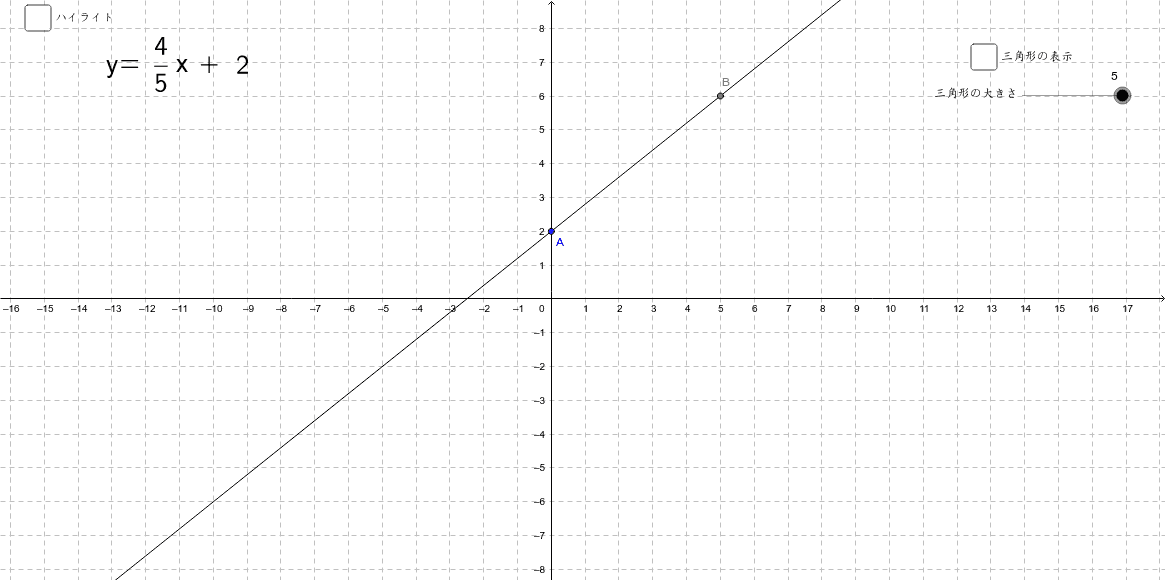
1次関数のグラフと式の関係 Geogebra
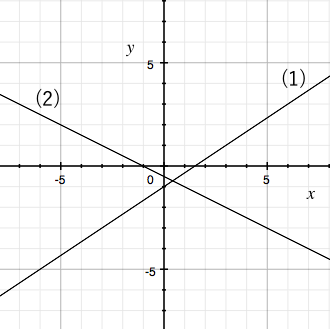
一次関数 グラフから関数の式を答える 苦手な数学を簡単に

一次関数のグラフ 無料で使える中学学習プリント

高校数学 絶対値付き1次関数のグラフ 受験の月
Mathematics 1次関数 3 1次関数のグラフ 働きアリ
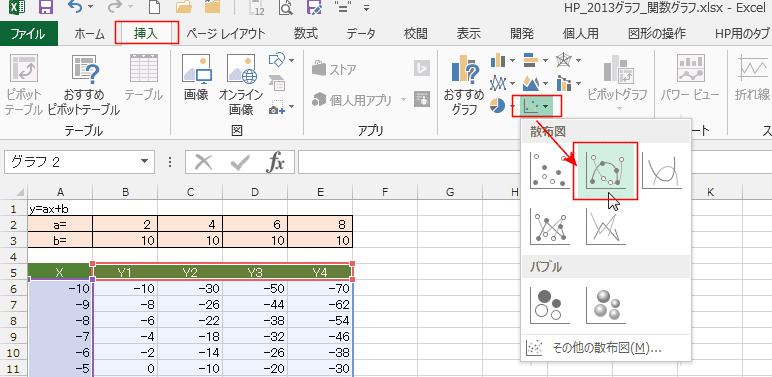
一次関数 二次関数のグラフや円のグラフを作成したい エクセル13基本講座
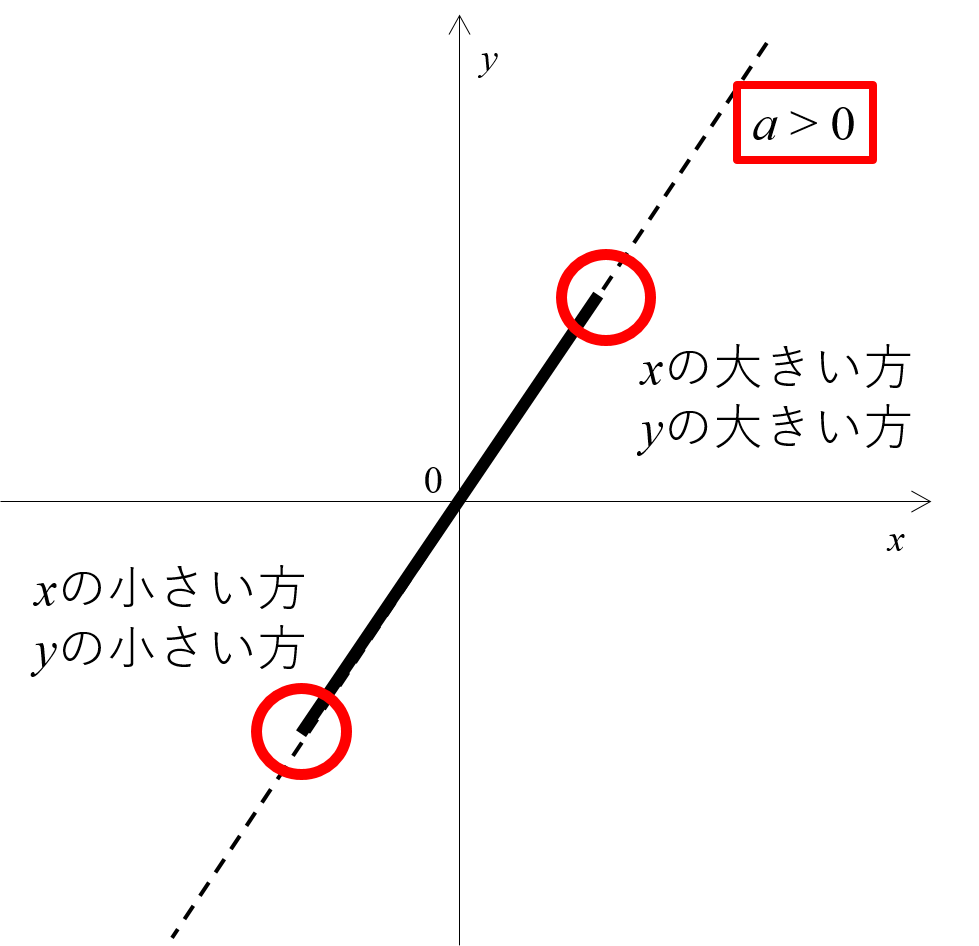
1次関数 変域を使った問題の解き方2 数学がわかるブログ
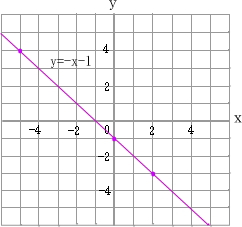
1次関数のグラフを描く 中学から数学だいすき
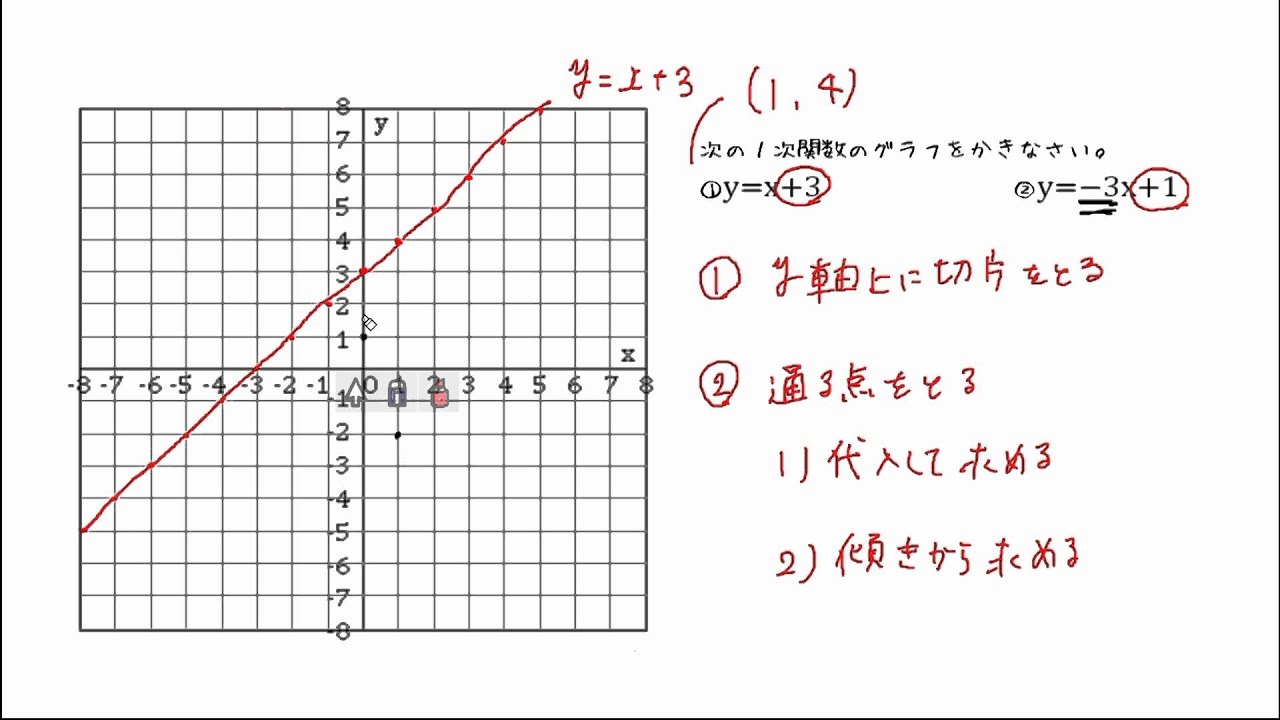
一次関数のグラフ 問題 Youtube

1次関数のグラフ 数学i フリー教材開発コミュニティ Ftext

一次関数はこれで完璧 グラフの書き方と変化の割合の求め方

1次関数の式とグラフ の問題のわからないを5分で解決 映像授業のtry It トライイット
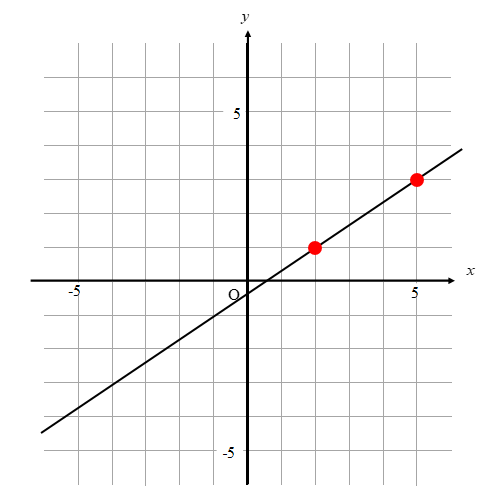
一次関数のグラフ 傾き 切片が分数 グラフの書き方を徹底解説 数スタ
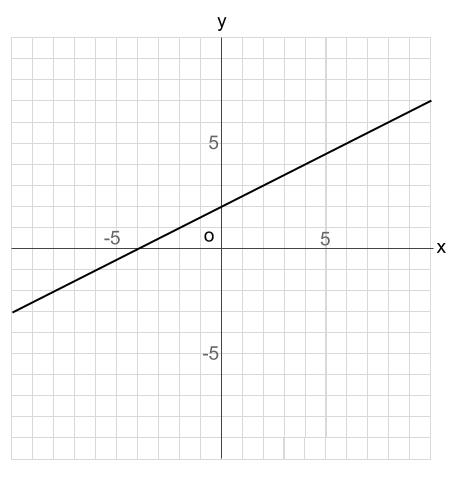
中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su
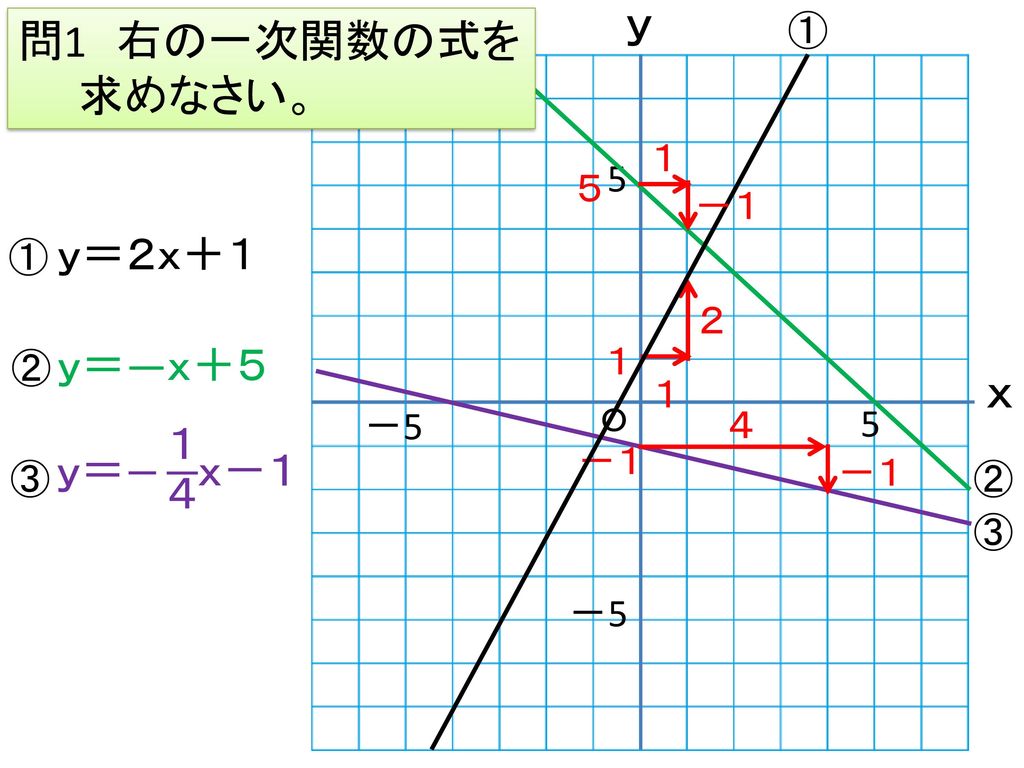
一次関数のグラフ 式を求めること 本時の流れ ねらい グラフや座標など与えられた条件をもとに一次 関数の式を求める Ppt Download

1次関数の応用 点の折り返し 生地伸ばし 1次関数 代数 中学数学 数学スキルをつけるturning Math トレ

一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ

1次不等式と1次関数の関係について 数学i フリー教材開発コミュニティ Ftext
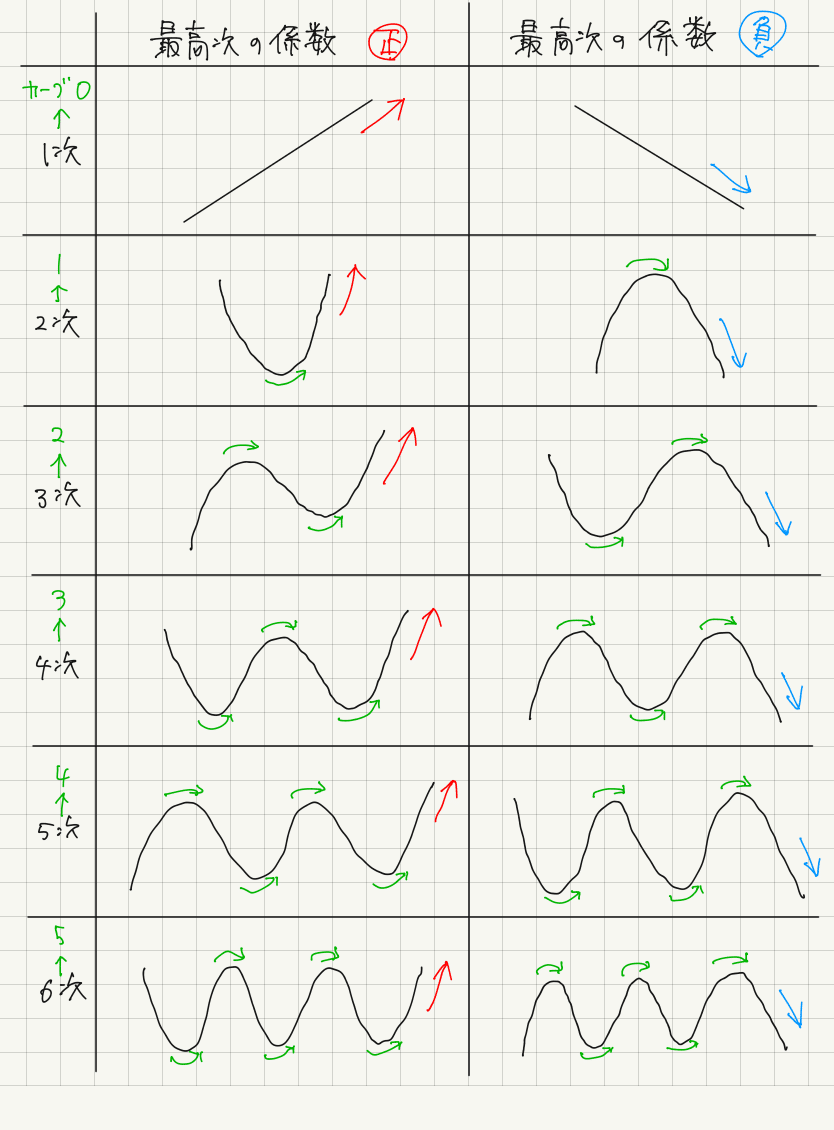
N次関数のグラフの概形 関谷 翔 Note
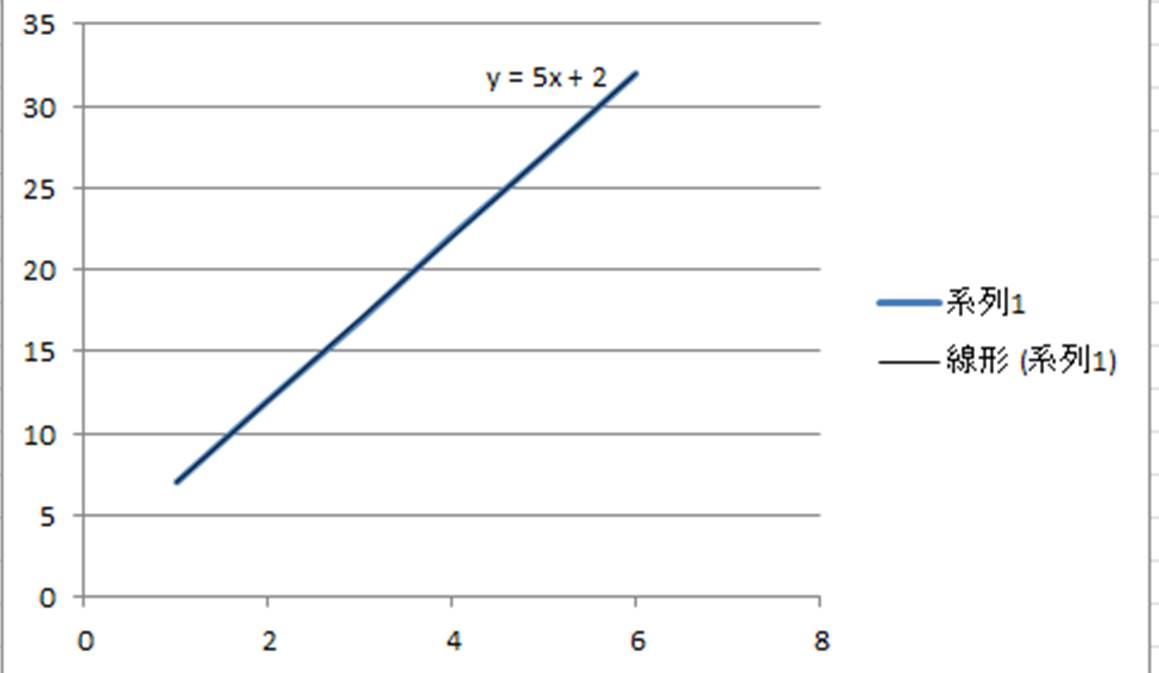
Excel エクセルで一次関数を計算し グラフを作る方法 一次関数の解を求める方法
Http Www2 Center Ibk Ed Jp Contents Jouhou Shidouan H22 11s Pdf 11s Tyoken 15kaneko Pdf
一次関数の利用を解説 グラフの書き方や解き方を知り入試に活かそう Studyplus スタディプラス
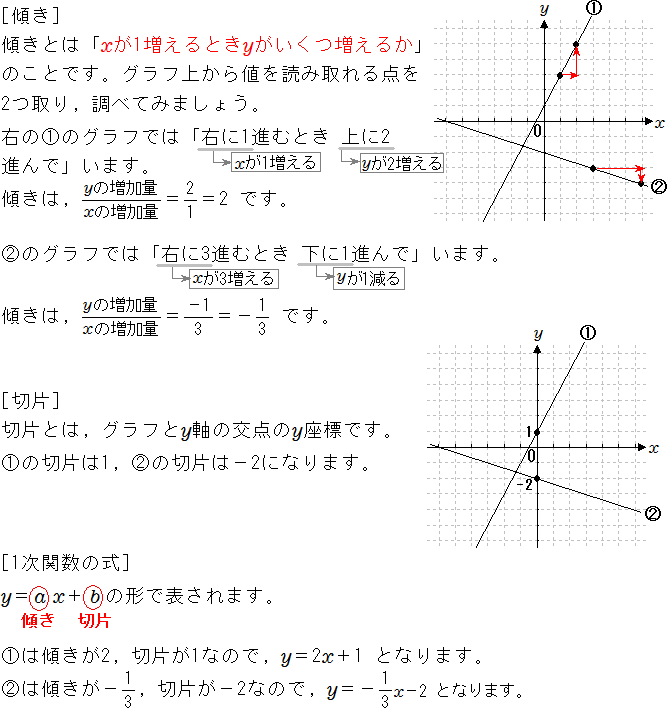
1次関数 1次関数のグラフの読み取りの基礎 中学数学 定期テスト対策サイト

中2数学 1次関数のグラフの書き方 例題編 映像授業のtry It トライイット
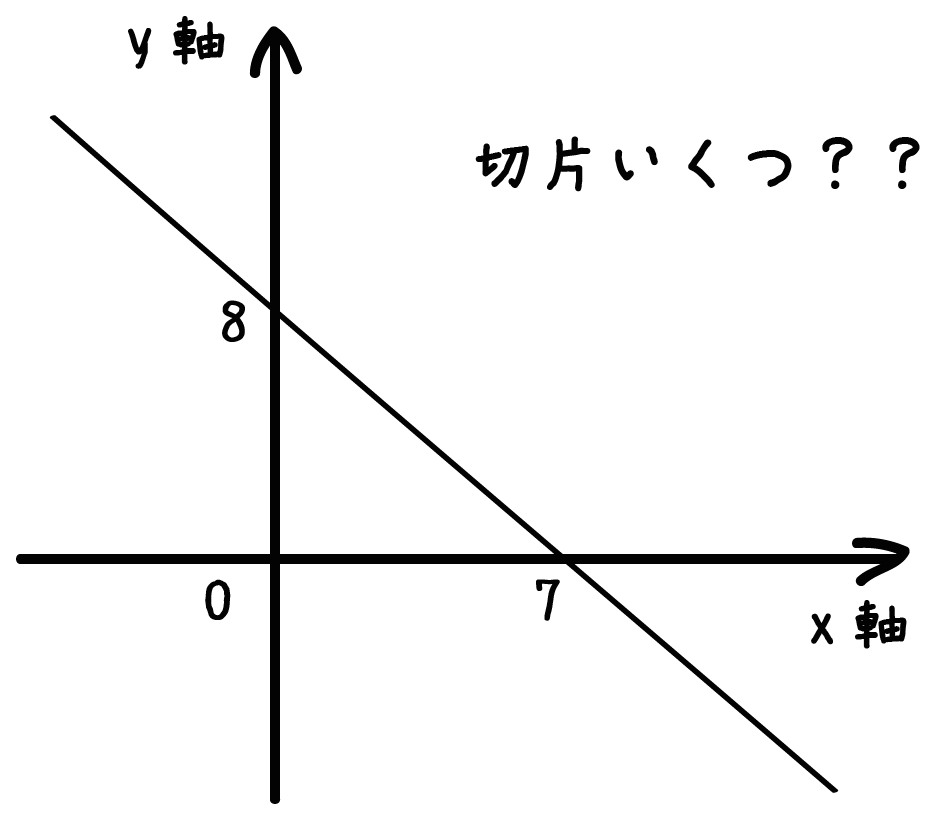
中2数学 一次関数の切片を求める2つの方法 Qikeru 学びを楽しくわかりやすく

切片が分数の時どうやってグラフを書くのかがわかりません 教えて欲しいです Clear

一次関数のグラフと変域の所で yの変域のグラフの書き方が分かりません Clear
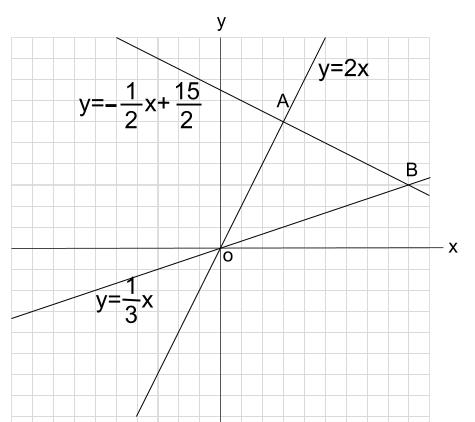
中学数学 1次関数と三角形の面積 その2 中学数学の無料オンライン学習サイトchu Su
方眼紙 5ミリ 10ミリ 数学の関数グラフ練習用 方眼ノート 無料ダウンロード ちびむすドリル 小学生
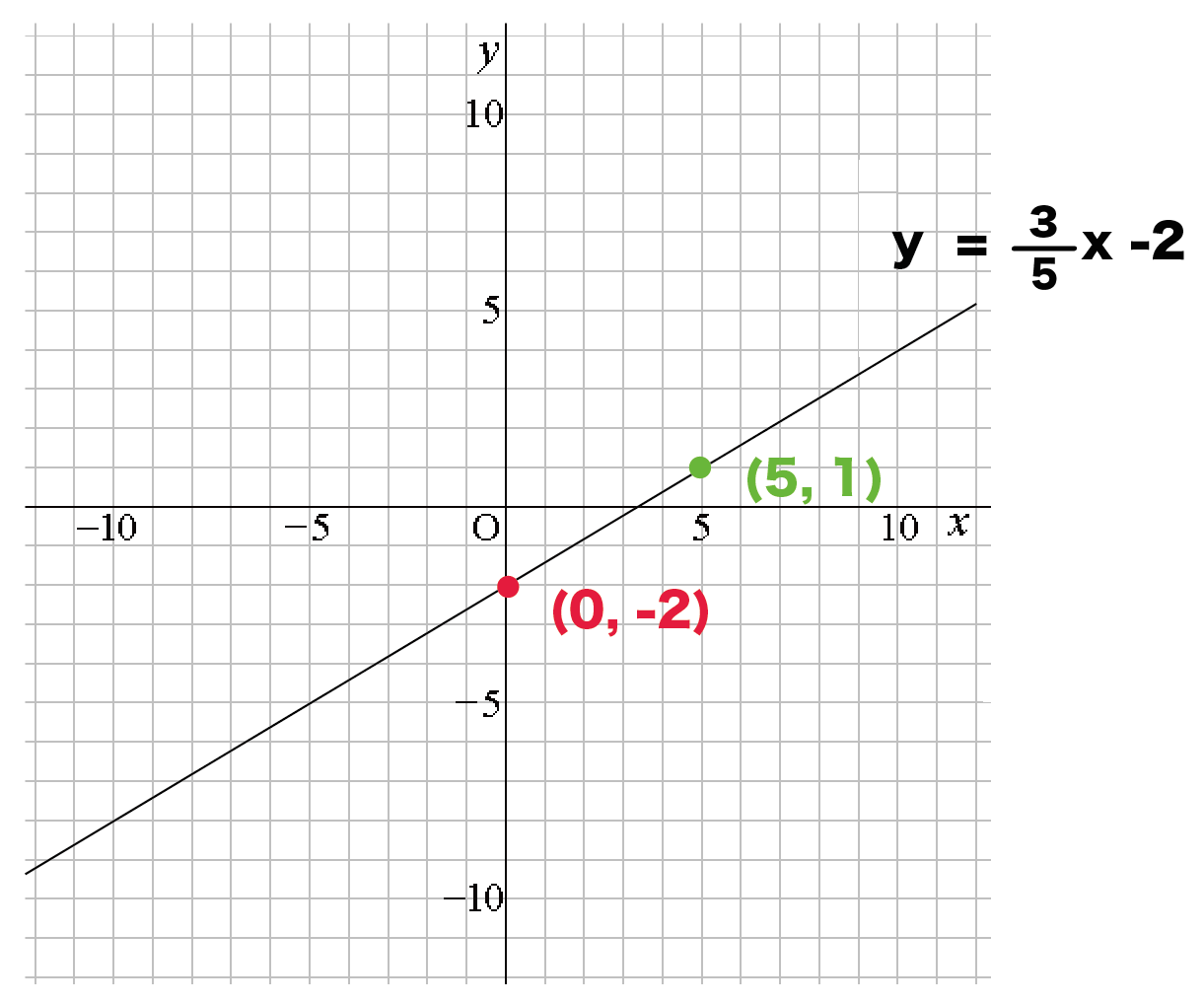
中2数学 一次関数のグラフの書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
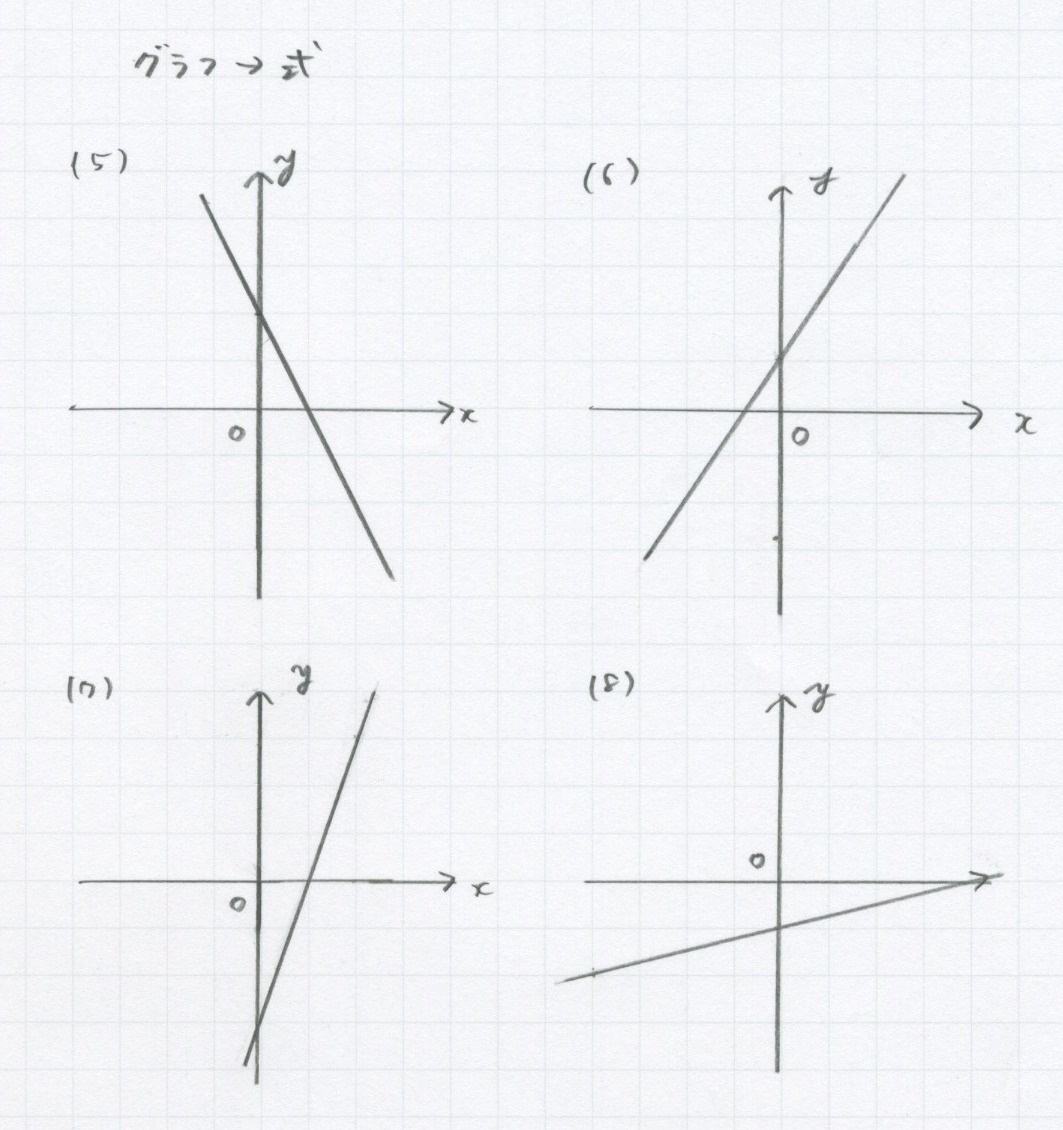
9 1 1次関数 グラフの描き方 読み取り方 勉強できようサイト

一次関数の問題の解き方 7パターン 数学fun

1次関数とそのグラフ 数学 二次関数 数学公式まとめ大全

中3数学 2次関数のグラフの特徴と練習問題
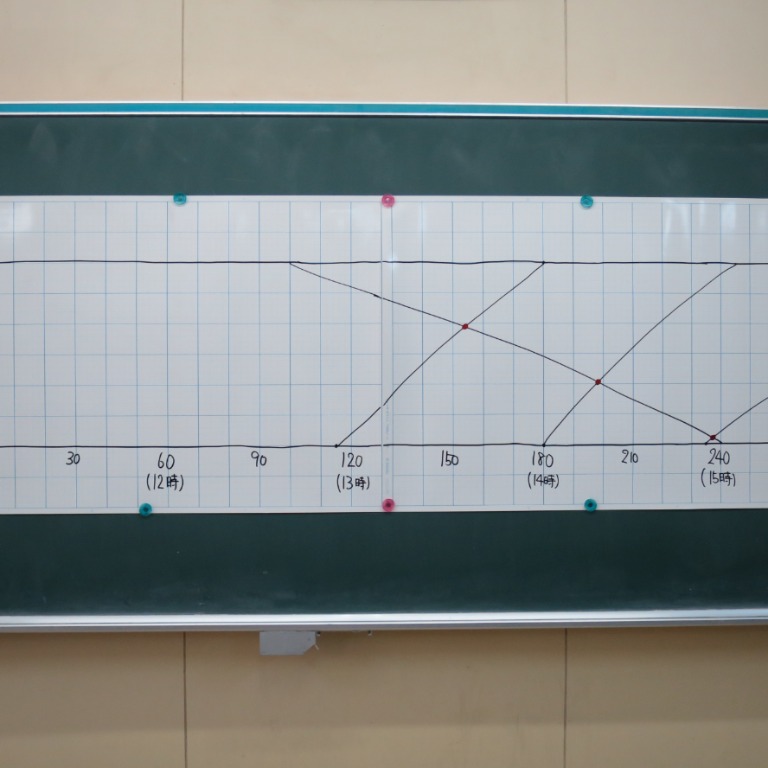
Tossランド 1次関数のグラフの利用

一次関数 グラフの書き方 切片が分数のときにはどうする Youtube
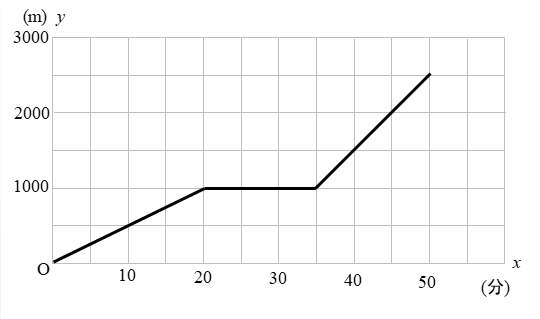
一次関数の利用 追いつく速さの文章問題を解説 数スタ
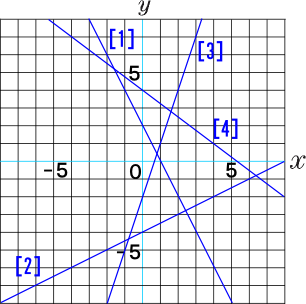
中学2年数学練習問題 一次関数の直線の式 傾き 切片 の求め方
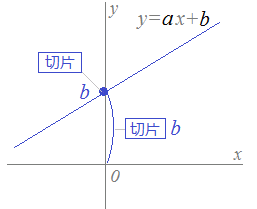
1次関数 グラフ 直線の方程式
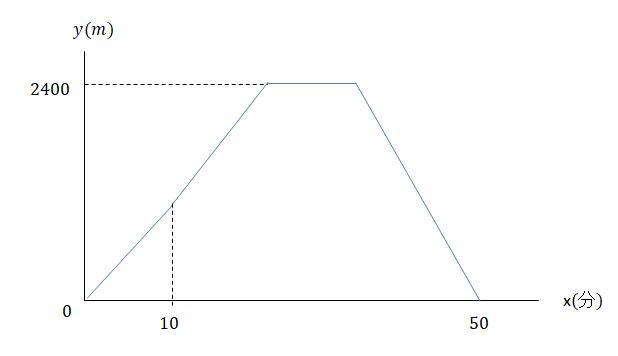
中2数学 一次関数の利用 距離 時間 速さ 対策練習問題 中学生勉強サイトあかね先生
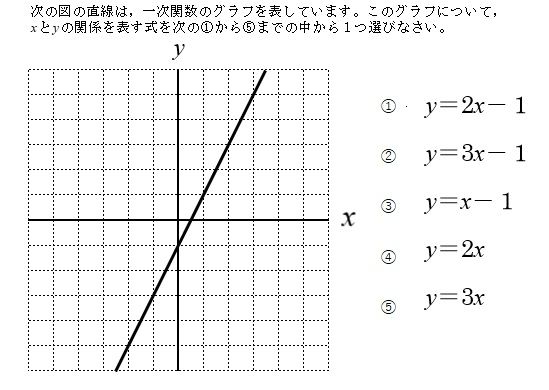
中2数学 一次関数のグラフ を作成 おっくうの教材作成日記 楽天ブログ
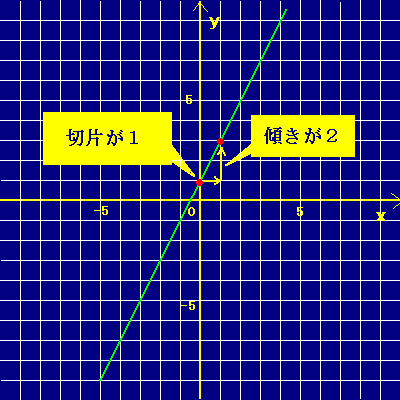
中2 1次関数4

一次関数を子供に教える

基本 一次不等式と一次関数のグラフ なかけんの数学ノート
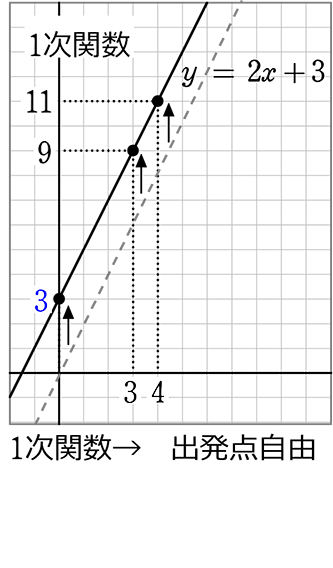
中学数学 一次関数

1次関数のグラフと1次不等式
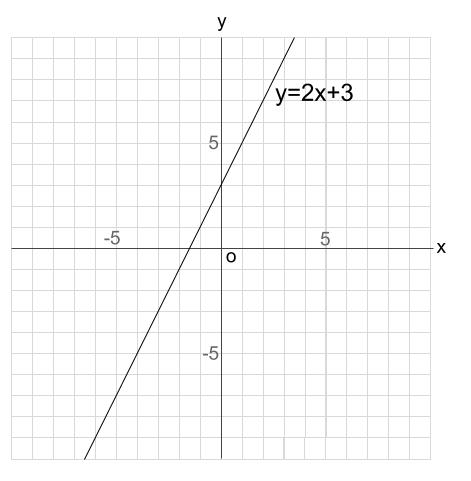
中学数学 1次関数のグラフ 中学数学の無料オンライン学習サイトchu Su
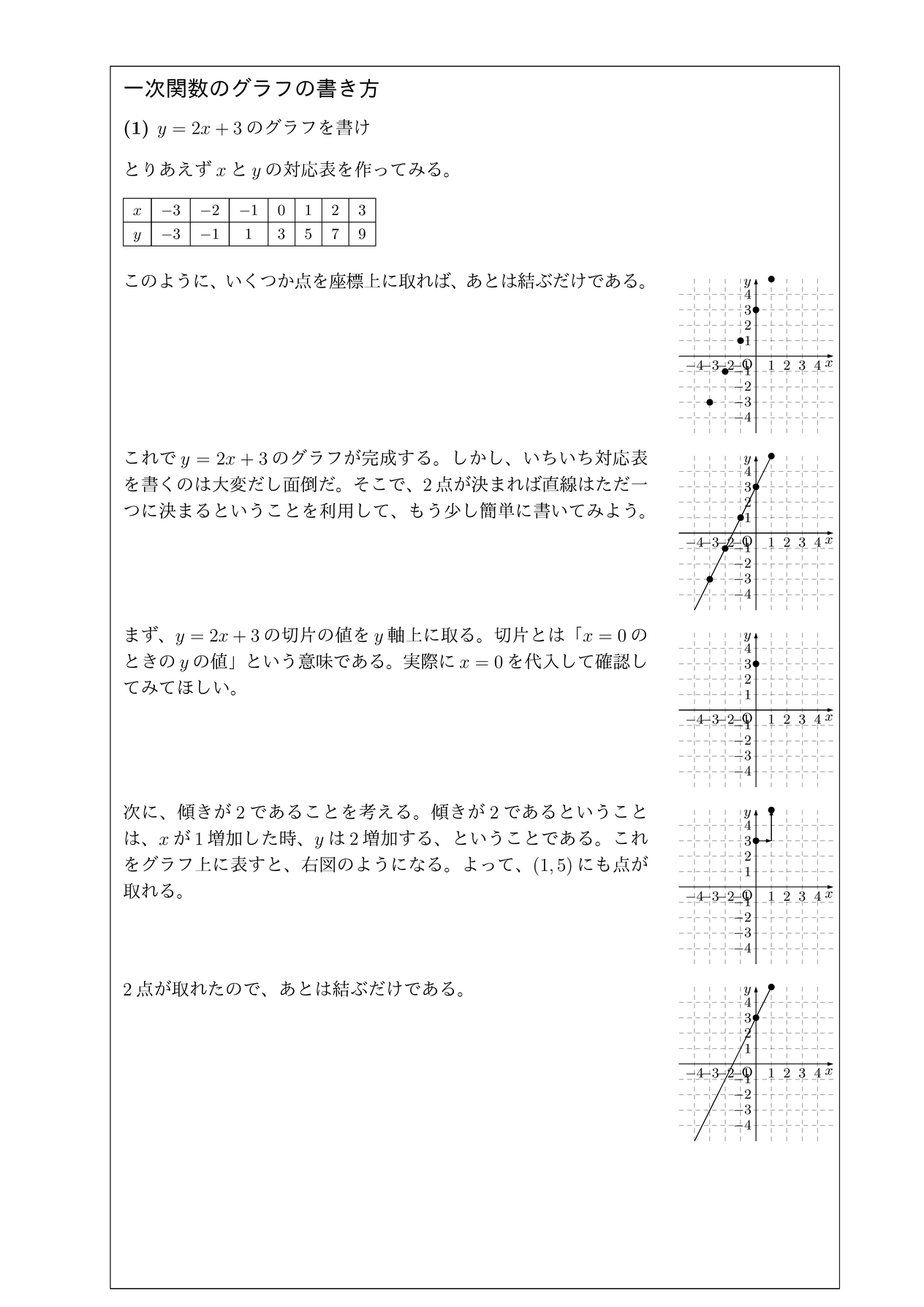
一次関数のグラフの書き方 チーム エン

数学中二 一次関数 方程式とグラフ 中学数学に関する質問 勉強質問サイト

一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ

関数用のグラフテンプレート素材 無料で使える中学学習プリント
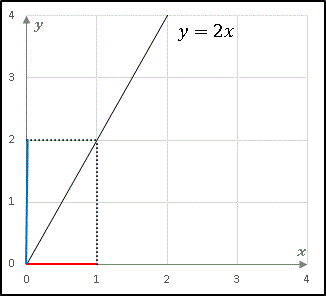
1次関数に潜む無限の真実

一次関数のグラフの利用1 無料で使える中学学習プリント

中学校数学 2年生 数量 一次関数 Wikibooks
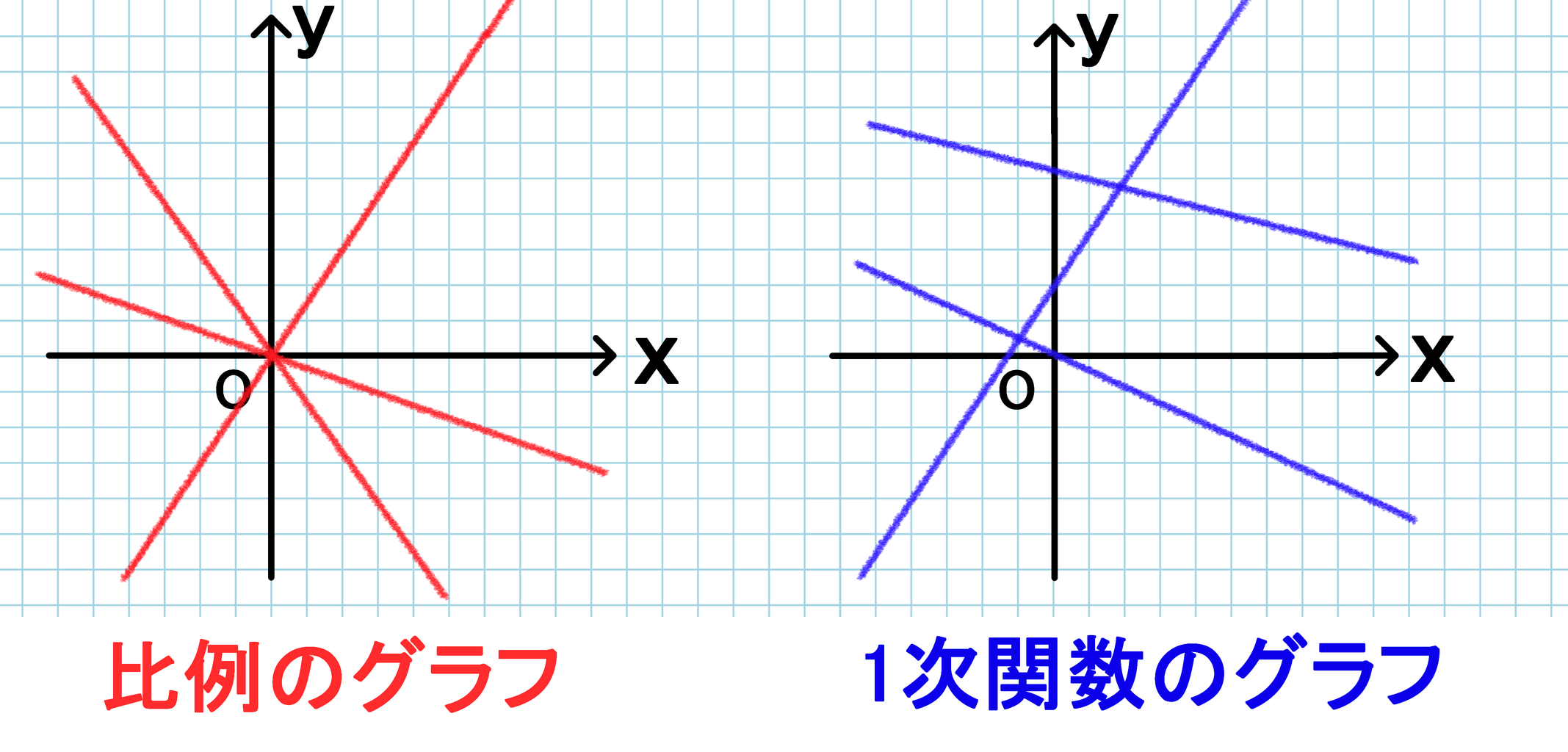
1次関数と比例の違いとは バカでもわかる 中学数学
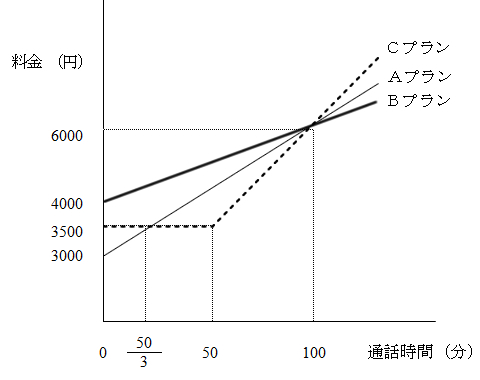
授業実践記録 数学 1次関数を利用して 携帯電話の一番お得なプランを選ぼう 啓林館
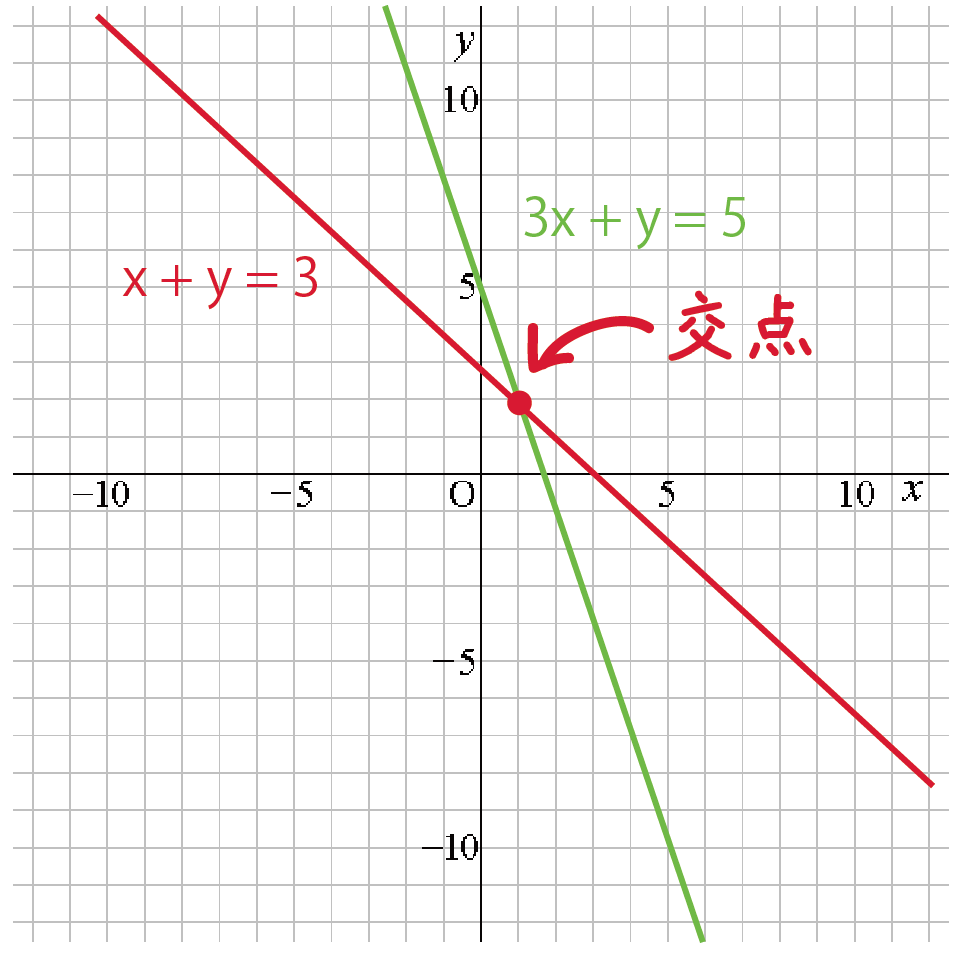
一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく
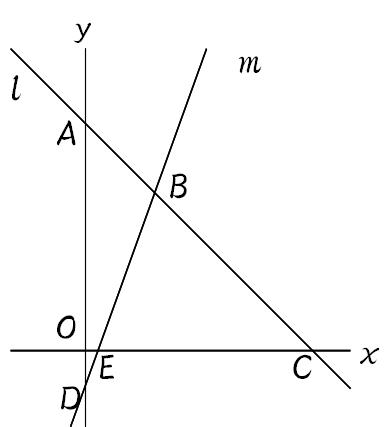
Mathematics 1次関数 6 応用問題の解き方 1 1次関数と図形 働きアリ
一次関数のグラフ 中学2年 数学クラブ
一次関数の利用を解説 グラフの書き方や解き方を知り入試に活かそう Studyplus スタディプラス



